About interval indexes

Under the cut we will investigate whether the need for indexing intervals, a special index how to be with multi-dimensional intervals, is it true that 2-dimensional rectangle can be treated as a 4-dimensional point, etc on the example of PostgreSQL.
The development of the theme (1, 2, 3, 4, 5, 6, 7).
Sometimes the data shows no values but, say, a confidence interval. Or is it really the value intervals. Again, the rectangle is the same interval that is one-dimensional. Is there an option for logarithmic time to check whether the data intervals that intersect with the search?
Yes, of course. Sometimes invent clever scheme the calculation and indexation of block (with a further fine filter) values, based on, for example, gray codes. The interval with the loss of precision is encoded in some (indexed) the number in the search interval gives rise to a set of values (pointervalue) that you should check. This set is limited to the logarithm.
But the GiST know how use for indexing time intervals (tsrange) R-trees.
the
create table reservations(during tsrange);
insert into reservations(during) values
('[2016-12-30, 2017-01-09)'),
('[2017-02-23, 2017-02-27)'),
('[2017-04-29, 2017-05-02)');
create index on reservations using gist(during);
select * from reservations where during && '[2017-01-01, 2017-04-01)';Of course, the author with his
So how R-tree copes with the intervals? As with other spatial objects. The interval is a one — dimensional rectangle, when the page splitting R-tree tries to minimize the variance inside pages-descendants and maximize the judges between them.
Is it possible to turn the interval to the point? Considering, for example, his start in X and end of Y. Formally, you can, after all, who can forbid us to use the two numbers as two-dimensional points? But such data have this internal dependence. And the semantics in the data will lead to a semantics in search queries and interpret results.
The easiest way to understand the situation, glancing at her eyes.
Here's 100 random intervals from 0 to 10 000 since the beginning of the interval from 0 to 100 000
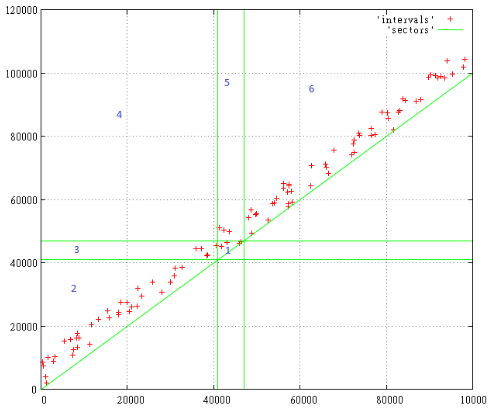
Fig.1
Search query — [41 000 47 000...], we are interested in all intervals that intersect with the specified range.
The numbers indicate the search area, which in this case arise. Everything below the diagonal, for obvious reasons, does not exist.
So, according to areas:
-
the
- here come the intervals that are strictly inside a search query
- these intervals started before and ended during a search query the
- here are the intervals that completely cover the search the
- these intervals began on time and ended after request
here everything began and ended before the desired interval the
here everything started and ended after it
Thus, to find all intersections of the query should be expanded to [0...47 000, 41 000... 100 000], i.e. it should include 1,3,4,5.
That request became the size of a quarter of the total layer should not scare you, after all, inhabited only a narrow strip along the diagonal. Yes, there may be large intervals of the size of the entire layer, but relatively little.
Of course, large objects will affect performance, but there's nothing you can do, because they do exist and do need to get the results for almost any query. If you try to index the “spaghetti monster”, the index will actually stop working, it would be cheaper to see the table and to clean up the excess.
Is there still some disadvantages of this approach? Because the data in some way "degenerated", perhaps the heuristic of splitting pages R-tree is less efficient. But the biggest inconvenience is that we must always have in mind that we are dealing with interval and set to the correct search queries.
However, this is not the R-tree, and to any spatial index. Including the Z-curve (constructed on a Z-order B-tree) used. For Z-curve does not matter the degeneration data, because it's just numbers with their natural order.
In addition, the Z-curve more and more compact R-tree. So we will try to clarify it to prospects in a designated area.
Here, for example, we assume that a X-coordinate is the beginning of the segment, and Y is the end. But what if the opposite? R-tree should be all the same, for Z-curve, too little will change. Bypass pages will be organized differently, but the number of pages read on average will be the same.
How about flipping the data on one axis. In the end, we have the same Z-curve (mirrored in Y), so let the data and lie on the diagonal crossbar the letter Z. Well, we conducted a numerical experiment.
Take 1000 random intervals and divide them into 10 pages depending on Z-values. Ie, sort them and divide by 100, then look what we've got. Prepare 2 sets — X,Y and max(X)-X, Y
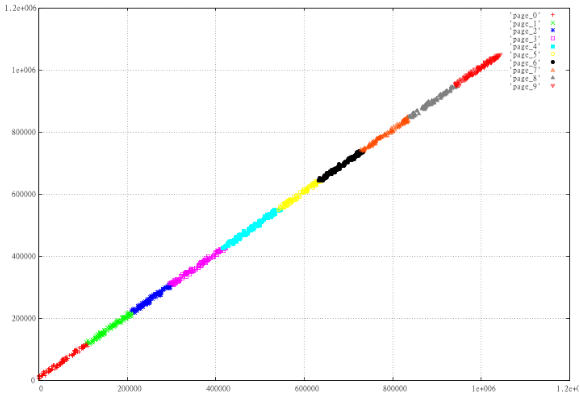
Fig.2 Regular Z-curve
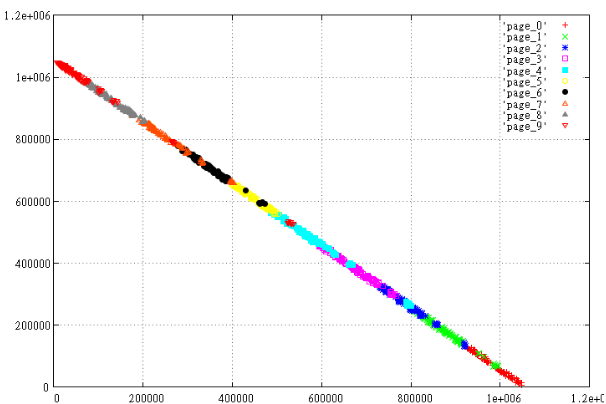
Fig.3 Mirrored data.
Nice to see how “worse” is arranged in the displayed data, the pages overlap each other, the perimeter of the pages a lot more, and it's a guarantee that on average, other things being equal, this option will read more pages.
Why did this happen? In this case, the reason is obvious. For 2-dimensional rectangle Z-value of lower left corner <= than the top right. Therefore, the ideal way to be careful to cut on the page is almost linear data is to place them along the line X=Y.
if the index is not the start-end range, and its center-length? In this case, the data will be pulled out along the X axis, as if we turned Fig.2 clockwise by 45 degrees. The problem is that in this search area that is rotated 45 degrees and it will be impossible to find a single query.
Can I index the intervals with more than one dimension? Of course. 2-dimensional rectangle turns into a 4-dimensional point. The main thing is not to forget which one of the coordinates that we put.
Can I mix intervals with newintervals values? Yes, because the search algorithm on the Z-curve does not know the semantics of the values, it works with faceless numbers. If the search extent is set in accordance with the semantics and interpretation of the results is her and her is no problem.
the
Numerical experiment
Try to check the operability of the Z-curve in conditions close to the “spaghetti monster”. The data model is as follows:
the
-
the
- 8-dimensional index, the health and performance of which we have already checked the
- as usual, 100 million points the
- objects are 3-dimensional parallelepipeds — is a 6-dimensional the
- of the remaining 2 dimensions we will give a time interval the
- parallelepipeds 100 pieces — they form in the X&Y grid of 10 x 10 the
- every box lives one unit of time the
- for each unit of time the box grows by 10 units along Z, starting with 0 height
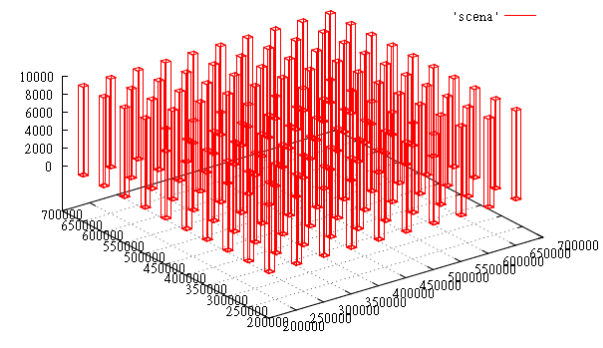
Fig.4 data slice at time T=1000
This test will check the indexing extended objects, how it affects search performance.
Create a 8-dimensional table, and fill data and index
the
create table test_points_8d (p integer[8]);
COPY test_points_8d from '/home/.../data.csv';
Order key: xmax,xmin,ymax,ymin,zmax,zmin,tmax,tmin.
the data file (data.csv):
the {210000,200000,210000,200000,0,0,0,0}
{210000,200000,210000,200000,10,0,1,1}
{210000,200000,210000,200000,20,0,2,2}
{210000,200000,210000,200000,30,0,3,3}
{210000,200000,210000,200000,40,0,4,4}
{210000,200000,210000,200000,50,0,5,5}
{210000,200000,210000,200000,60,0,6,6}
{210000,200000,210000,200000,70,0,7,7}
{210000,200000,210000,200000,80,0,8,8}
{210000,200000,210000,200000,90,0,9,9}
...
Test query [200 000...300 000; 200 000 ... 300 000; 100...1000; 10...11]:
the select c, t_row from (select c, (select p from test_points_8d t where c = t.ctid) t_row
from zcurve_8d_lookup_tidonly('zcurve_test_points_8d',
200000,0,200000,0,100,0,10,0,
1000000,300000,1000000,300000,1000000,1000,1000000,11
) as c) x;
The answer is:
the c | t_row
-------------+-------------------------------------------
(0,11) | {210000,200000,210000,200000,100,0,10,10}
(0,12) | {210000,200000,210000,200000,110,0,11,11}
(103092,87) | {260000,250000,210000,200000,100,0,10,10}
(103092,88) | {260000,250000,210000,200000,110,0,11,11}
(10309,38) | {210000,200000,260000,250000,100,0,10,10}
(10309,39) | {210000,200000,260000,250000,110,0,11,11}
(113402,17) | {260000,250000,260000,250000,100,0,10,10}
(113402,18) | {260000,250000,260000,250000,110,0,11,11}
(206185,66) | {310000,300000,210000,200000,100,0,10,10}
(206185,67) | {310000,300000,210000,200000,110,0,11,11}
(216494,93) | {310000,300000,260000,250000,100,0,10,10}
(216494,94) | {310000,300000,260000,250000,110,0,11,11}
(20618,65) | {210000,200000,310000,300000,100,0,10,10}
(20618,66) | {210000,200000,310000,300000,110,0,11,11}
(123711,44) | {260000,250000,310000,300000,100,0,10,10}
(123711,45) | {260000,250000,310000,300000,110,0,11,11}
(226804,23) | {310000,300000,310000,300000,100,0,10,10}
(226804,24) | {310000,300000,310000,300000,110,0,11,11}
(18 rows)
What good is a data model, you can easily assess the correctness of the result.
The fresh-raised server the same query using EXPLAIN (ANALYZE,BUFFERS)
shows: read 501 page.
OK, move the index. But if one were to look at the same query on the index order key,xmin,ymin, zmin,xmax,ymax,zmax,tmin,tmax. The launch shows 531 reading. A bit too much.
Well, remove geometric distortion, suppose now that the columns do not grow at 10 and 1 unit per tick. Query (key: xmax,xmin,ymax,ymin,zmax,zmin,tmax,tmin)
the EXPLAIN (ANALYZE,BUFFERS) select c, t_row from (select c, (select p from test_points_8d t where c = t.ctid) t_row
from zcurve_8d_lookup_tidonly('zcurve_test_points_8d',
200000,0,200000,0,0,0,10,0,
1000000,300000,1000000,300000,1000000,1000,1000000,11) as c) x;
said that it read 156 pages!
Now some statistics, look at the average number of reads/cache hits for different types of keys in a series of 10 000 random queries
size 100 000Х100 000Х100 000Х10
When you order key
(xmin,1 000 000-xmax, ymin,1 000 000-ymax,zmin,1 000 000-zmax,tmin,1 000 000-tmax)
The average number of readings 21.8217, cache hits — 2437.51.
The average number of objects in the results — 17.81
When you order key — (xmax,xmin,ymax,ymin,zmax,zmin,tmax,tmin)
The average number of readings 14.2434, cache hits — 1057.19.
The average number of objects in the results — 17.81
When you order key (xmin,xmax,ymin,ymax,zmin,zmax,tmin,tmax)
The average number of readings 14.0774, cache hits — 1053.22.
The average number of objects in the results — 17.81
As you can see, the page cache in this case works very effectively. A number of the readings are acceptable.
And finally, look at the eyes, just out of curiosity, how algorithm Z-curve to cope with the 8-dimensional space.
Below are the projections of the parsed query in the extent
[200 000...300 000; 200 000 ... 300 000; 0...700 001; 700 000...700 001].
A total of 18 results, 1687 subqueries. Shows the generated subqueries, green crosses, read in the B-tree, blue TIC results.
Under each cross can hide a few marks. Merge closely spaced markers, such as time and 700 000 700 001.

Fig.5 X-axis

Fig.6 Y-axis
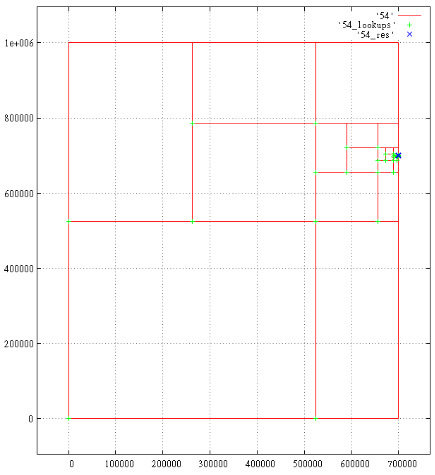
Fig.7 Z-axis

Fig.8 Time
Комментарии
Отправить комментарий